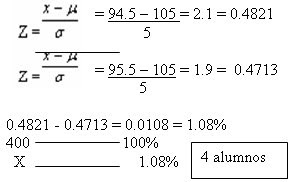viernes, 3 de octubre de 2008
COMETARIO BLOG
martes, 30 de septiembre de 2008
EJEMPLO DE TEORIA DE CONTEO.
En una caja hay 4 esferas de diferentes colores (azul, verde rojo y negro) si se extrae una esfera a la vez, hallar el numero de posibilidades de extracción.

COMENTARIO: La teoria de conteo mas que todo nos da a conocer las formas diferentes de contar presentandose varias respuestas como el fenomeno que se nos detallo anteriormente.
EJEMPLO DE TEORIA DE CONTEO.
En una caja hay 4 esferas de diferentes colores (azul, verde rojo y negro) si se extrae una esfera a la vez, hallar el numero de posibilidades de extracción.
 COMENTARIO: la teoria de conteo basicamente es la forma de obtener distintos resultados de un problema de una forma distinta en donde el fenomeno dado presenta varios resultados.
COMENTARIO: la teoria de conteo basicamente es la forma de obtener distintos resultados de un problema de una forma distinta en donde el fenomeno dado presenta varios resultados.lunes, 29 de septiembre de 2008
http://www.youtube.com/results?search_query=videos+de+probabilidad&search_type
miércoles, 24 de septiembre de 2008
En estadística la esperanza matemática (o simplemente esperanza) o valor esperado de una variable aleatoria es la suma del producto de la probabilidad de cada suceso por el valor de dicho suceso. Por ejemplo, en un juego de azar el valor esperado es el beneficio medio.
Si todos los sucesos son de igual probabilidad la esperanza es la media aritmética.
Con frecuencia es conveniente calcular el promedio de los resultados o experimentos, ponderado por la probabilidad de que suceda cada uno de los resultados posibles .
La esperanza matematica permite comparar dos o mas alternativas. la sumatoria de la esperanza matematica seria de la siguiente forma:

COMENTARIO: La esperanza matematica suelen ser los resultados diferentes de distintos eventos mas bien una media, y podemos comparar los mejores resultados que podamos obtener.
domingo, 21 de septiembre de 2008
ARBOL DE PROBABILIDAD
Es una grafica que representa los resultados posibles de un evento así como la posibilidad de ocurrencia.
En una fabrica de alfileres logra una producción con solo 1% de alfileres defectuosos. Prepare un arbol de probabilidad para 2 alfileres tomados aleatoriamentes.

COMENTARIO: el arbol de probabilidades nos va a dar a conocer los posibles resultados de los eventos a realizar o asi tambien las formas en que pueden ocurrir.
sábado, 20 de septiembre de 2008
Un axioma, en epistemología, es una "verdad evidente" que no requiere demostración, pues se justifica a sí misma, y sobre la cual se construye el resto de conocimientos por medio de la deducción; aunque, no todos los epistemólogos están de acuerdo con esta definición "clásica". El axioma gira siempre sobre sí mismo, mientras los postulados y conclusiones posteriores se deducen de este.
En matemática, un axioma no es necesariamente una verdad evidente, sino una expresión lógica utilizada en una deducción para llegar a una conclusión.
Etimología
La palabra axioma proviene del griego αξιωμα (axioma), que significa "lo que parece justo" o aquello que es considerado evidente y sin necesidad de demostración. La palabra viene del griego αξιοειν (axioein) que significa "valorar", que a su vez procede de αξιος (axios) que significa "valuable" o "digno". Entre los antiguos filósofos griegos, un axioma era aquello que parecía ser verdadero sin ninguna necesidad de prueba.
Lógica
La lógica del axioma es partir de una premisa calificada verdadera por sí misma (el axioma) e inferir sobre esta otras proposiciones por medio del método deductivo, obteniendo conclusiones coherentes con el axioma. Los axiomas han de cumplir sólo un requisito: de ellos, y sólo de ellos, han de deducirse todas las demás proposiciones de la teoría dada.
Limitaciones
Kurt Gödel demostró a mediados del siglo XX que los sistemas axiomáticos de cierta complejidad, por definidos y consistentes que sean, poseen serias limitaciones. En todo sistema de una cierta complejidad, siempre habrá una proposición P que sea verdadera, pero no demostrable. De hecho, Gödel prueba que, en cualquier sistema formal que incluya la aritmética, puede formarse una proposición P que afirme que este enunciado no es demostrable. Si se pudiera demostrar P, el sistema sería contradictorio: no sería consistente. Luego P no es demostrable y, por tanto, P es verdadero.
Matemáticas:
En lógica matemática, un axioma no es necesariamente una verdad evidente, sino una expresión lógica utilizada en una deducción para llegar a una conclusión. En matemática se distinguen dos tipos de axiomas: axiomas lógicos y axiomas no-lógicos.
Axiomas lógicos
Éstas son ciertas fórmulas en un lenguaje que son universalmente válidas, esto es, fórmulas que son satisfechas por cualquier estructura y por cualquier función variable, en términos coloquiales, éstos son enunciados que son verdaderos en cualquier universo posible, bajo cualquier interpretación posible y con cualquier asignación de valores. Usualmente uno toma como axiomas lógicos un conjunto mínimo de tautologías que es suficiente para probar todas las tautologías en el lenguaje
Axiomas no-lógicos
Los Axiomas no-lógicos son fórmulas específicas de una teoría y se aceptan solamente por acuerdo. Razonando acerca de dos estructuras diferentes, por ejemplo, los números naturales y los números enteros puede involucrar a los mismos axiomas lógicos, sin embargo, los axiomas no-lógicos capturan lo que es especial acerca de una estructura en particular (o un conjunto de estructuras). Por lo tanto los axiomas no-lógicos, a diferencia de los axiomas lógicos, no son tautologías. Otro nombre para los axiomas no-lógicos es postulado.
Casi cualquier teoría matemática moderna se fundamenta en un conjunto de axiomas no-lógicos, se pensaba que en principio cualquier teoría puede ser axiomatizada y formalizada, posteriormente esto se demostró imposible.
En el discurso matemático a menudo se hace referencia a los axiomas no-lógicos simplemente como axiomas, esto no significa que sean verdaderos en un sentido absoluto. Por ejemplo en algunos grupos, una operación puede ser conmutativa y esto puede ser afirmado introduciendo un axioma adicional, pero aún sin la introducción de este axioma se puede desarrollar la teoría de grupos e incluso se puede tomar su negación como un axioma para estudiar los grupos no-conmutativos.
Un axioma es el elemento básico de un sistema de lógica formal y junto con las reglas de inferencia definen un sistema deductivo.
Un evento es el resultado posible o un grupo de resultados posibles de un experimento y es la mínima unidad de análisis para efectos de cálculos probabilísticas los eventos se clasifican de la siguiente forma:
MUTUAMENTE EXCLUYENTE: Aquellos que no pueden ocurrir al mismo tiempo ejemplo: “CARA o ESCUDO”
INDEPENDIENTES: estos no se ven afectados por otros. Ejemplos:
“color de zapatos, blusas o la probabilidad de que llueva hoy”
DEPENDIENTE: cuando un evento afecta la probabilidad de ocurrencia de otros. “Repaso-calificaciones”
NO EXCLUYENTE ENTRE SI: cuando la ocurrencia de uno de ellos no impide que ocurra el otro ej. Que una personas sea doctor y que tenga 50 años”, “un estudiante que este casado”
Cuando el enunciado de un problema de probabilidad tiene como condicion que se presente uno u otro evento la probabilidad total se forma por la suma directa de las probabilidades.
P ( A o B) = P(A) + P (B)
En el caso de eventos no excluyentes entre si debe considerarse que la probabilidad de que ocurran ambos eventos esta incluida en ellos esa probabilidad de sumas directas.
REGLA GENERAL DE LA SUMA DE PROBABILIDADES:
P (A o B) = P(A) + P(B) – P(A y B)
Cuando el enunciado de un problema de probabilidad tiene como condicion que se presente uno y otro la probabilidad total se forma por la multiplicación directa de las probabilidades individuales se los eventos son independientes.
P (A Y B) = P (A) * P (B): (Si son independientes)
Si los eventos son dependientes debe considerarse que ocurra un segundo evento si ya ocurrió un primer evento, esto se conoce como REGLA GENERAL DE LA MULTIPLICACION DE PROBABILIDADES.
P(A y B) = P(A) * P (B / B )
EJEMPLOS DE EVENTOS MUTUAMENTE EXCLUYENTES.
Una caja contiene 8 tarjetas de color verde; 5 de color rojo y 1 de color celeste. Hallar la probabilidad de que al extraer aleatoriamente una tarjeta sea de color rojo
P(tr) = . 5 . = 5 = 0.36
8 + 5 + 1 14
EJEMPLO DE EVENTOS INDEPENDIENTES:
Una caja contiene 8 tarjetas de color verde; 5 de color rojo y 1 de color celeste. Determine la probabilidad de que al extraer al azar uno de estas tarjetas sea color roja y celeste.
P(r ó c) = 5 + 1 = 0.36 + 0.07
14 14
EJEMPLO DE PROBABILIDAD DEPENDIENTE
Una caja contiene 8 tarjetas de color verde; 5 de color rojo y 1 de color celeste. Hallar la probabilidad de que al extraer 2 tarjetas ambos sean de color verde.
P(8) = 8/14 = 0.57
P(7) = 7/14 = 0.5
P(8) * P(5) = 0.57 * 0.5= 0.285
COMENTARIO: axioma en consecuencia es la forma de la obtencion de resultados estos pueden ocurrir dependiendo de varios factores pueden incluirse varias caracteristicas para que el resultado varie al obtenerse.
lunes, 15 de septiembre de 2008
LA PROBABILIDAD
Relación entre números resultado de éxitos respecto al total de resultados posibles) puede ser SUBJETIVA O OBJETIVA. La primera refleja la percepción de quien la emite y la segunda es el resultado de cálculos.
La PROBABILIDAD OBJETIVA bajo el enfoque clasico supone que todos los eventos tiene la misma probabilidad de ocurrir. Por ejemplo.
Si en una caja existe 50 manzanas 200 naranjas ¿cual es la probabilidad de que al hacer una extracción sea una naranja
P(N) = 200 /200+50 = 200/250 = 0.80 80%
EJEMPLO DE LA PROBABILIDAD SUBJETIVA:
Existen naranjas y manzanas si se extraen 80 naranjas de 100 extracciones ¿CUAL ES LA PROBABILIDAD DE QUE SEAN NARANJAS?
P(N) = 80/100 = 0.8 80%
miércoles, 10 de septiembre de 2008
EJEMPLO DE TEORIA DE CONTEO.
En una caja hay 4 esferas de diferentes colores (azul, verde rojo y negro) si se extrae una esfera a la vez, hallar el numero de posibilidades de extracción.

COMENTARIO: basicamente Teoria de conteo son las distintas formas en que pueden obtenerse resultados distintos en un problema o fenomeno, como el expuesto anteriormente.
martes, 26 de agosto de 2008
Es todo arreglo de elementos en donde nos interesa el lugar o posición que ocupa cada uno de los elementos que constituyen dicho arreglo.
Para ver de una manera objetiva la diferencia entre una combinación y una permutación, plantearemos cierta situación.
Suponga que un salón de clase está constituido por 35 alumnos. a) El maestro desea que tres de los alumnos lo ayuden en actividades tales como mantener el aula limpia o entregar material a los alumnos cuando así sea necesario.
b) El maestro desea que se nombre a los representantes del salón (Presidente, Secretario y Tesorero).
Solución:
a) Suponga que por unanimidad se ha elegido a Daniel, Arturo y a Rafael para limpiar el aula o entregar material, (aunque pudieron haberse seleccionado a Rafael, Daniel y a Enrique, o pudo haberse formado cualquier grupo de tres personas para realizar las actividades mencionadas anteriormente).
¿Es importante el orden como se selecciona a los elementos que forma el grupo de tres personas?
Reflexionando al respecto nos damos cuenta de que el orden en este caso no tiene importancia, ya que lo único que nos interesaría es el contenido de cada grupo, dicho de otra forma, ¿quiénes están en el grupo? Por tanto, este ejemplo es una combinación, quiere decir esto que las combinaciones nos permiten formar grupos o muestras de elementos en donde lo único que nos interesa es el contenido de los mismos.
COMENTARIO: Las permutaciones son eventos sucesivos en donde nos va a importar el orden que este tenga.
COMBINACIÓN:
Es todo arreglo de elementos en donde no nos interesa el lugar o posición que ocupa cada uno de los elementos que constituyen dicho arreglo.
COMENTARIO: como nos dice claramente en el anterior enunciado en este caso el orden de los resultados no nos interesa el orden de las posibles resultados.
sábado, 16 de agosto de 2008
La probabilidad mide la frecuencia con la que ocurre un resultado en un experimento bajo condiciones suficientemente estables. La teoría de la probabilidad se usa extensamente en áreas como la estadística, la matemática, la ciencia y la filosofía para sacar conclusiones sobre la probabilidad de sucesos potenciales y la mecánica subyacente de sistemas complejos.
Interpretaciones
La palabra probabilidad no tiene una definición consistente. De hecho hay dos amplias categorías de interpretaciones de la probabilidad: los frecuentistas hablan de probabilidades sólo cuando se trata de experimentos aleatorios bien definidos. La frecuencia relativa de ocurrencia del resultado de un experimento, cuando se repite el experimento, es una medida de la probabilidad de ese suceso aleatorio. Los bayesianos, no obstante, asignan las probabilidades a cualquier declaración, incluso cuando no implica un proceso aleatorio, como una manera de representar su verosimilitud subjetiva.
Historia
Según Richard Jeffrey, "Antes de la mitad del siglo XVII, el término 'probable' (en latín probable) significaba aprobable, y se aplicaba en ese sentido, unívocamente, a la opinión y a la acción. Una acción u opinión probable era una que las personas sensatas emprenderían o mantendrían, en las circunstancias
Aparte de algunas consideraciones elementales hechas por Girolamo Cardano en el siglo XVI, la doctrina de las probabilidades data de la correspondencia de Pierre de Fermat y Blaise Pascal (1654). Christiaan Huygens (1657) le dio el tratamiento científico conocido más temprano al concepto. Ars Conjectandi (póstumo, 1713) de Jakob Bernoulli y Doctrine of Chances (1718) de Abraham de Moivre trataron el tema como una rama de las matemáticas. Véase El surgimiento de la probabilidad (The Emergence of Probability) de Ian Hacking para una historia de los inicios del desarrollo del propio concepto de probabilidad matemática.
La teoría de errores puede trazarse atrás en el tiempo hasta Opera Miscellanea (póstumo, 1722) de Roger Cotes, pero una memoria preparada por Thomas Simpson en 1755 (impresa en 1756) aplicó por primera vez la teoría para la discusión de errores de observación. La reimpresión (1757) de esta memoria expone los axiomas de que los errores positivos y negativos son igualmente probables, y que hay ciertos límites asignables dentro de los cuales se supone que caen todos los errores; se discuten los errores continuos y se da una curva de la probabilidad.
Pierre-Simon Laplace (1774) hizo el primer intento para deducir una regla para la combinación de observaciones a partir de los principios de la teoría de las probabilidades. Representó la ley de la probabilidad de error con una curva y = φ(x), siendo x cualquier error e y su probabilidad, y expuso tres propiedades de esta curva:
es simétrica al eje y;
el eje x es una asíntota, siendo la probabilidad del error igual a 0;
la superficie cerrada es 1, haciendo cierta la existencia de un error.
Dedujo una fórmula para la media de tres observaciones. También obtuvo (1781) una fórmula para la ley de facilidad de error (un término debido a Lagrange, 1774), pero una que llevaba a ecuaciones inmanejables. Daniel Bernoulli (1778) introdujo el principio del máximo producto de las probabilidades de un sistema de errores concurrentes.
El método de mínimos cuadrados se debe a Adrien-Marie Legendre (1805), que lo introdujo en su Nouvelles méthodes pour la détermination des orbites des comètes (Nuevos métodos para la determinación de las órbitas de los cometas). Ignorando la contribución de Legendre, un escritor irlandés estadounidense, Robert Adrain, editor de "The Analyst" (1808), dedujo por primera vez la ley de facilidad de error,
siendo c y h constantes que dependen de la precisión de la observación. Expuso dos demostraciones, siendo la segunda esencialmente la misma de John Herschel (1850). Gauss expuso la primera demostración que parece que se conoció en Europa (la tercera después de la de Adrain) en 1809. Demostraciones adicionales se expusieron por Laplace (1810, 1812), Gauss (1823), James Ivory (1825, 1826), Hagen (1837), Friedrich Bessel (1838), W. F. Donkin (1844, 1856) y Morgan Crofton (1870). Otros personajes que contribuyeron fueron Ellis (1844), De Morgan (1864), Glaisher (1872) y Giovanni Schiaparelli (1875). La fórmula de Peters (1856) para r, el error probable de una única observación, es bien conocida.
En el siglo XIX, los autores de la teoría general incluían a Laplace, Sylvestre Lacroix (1816), Littrow (1833), Adolphe Quetelet (1853), Richard Dedekind (1860), Helmert (1872), Hermann Laurent (1873), Liagre, Didion, y Karl Pearson. Augustus De Morgan y George Boole mejoraron la exposición de la teoría.
En la parte geométrica (véase geometría integral) los colaboradores de The Educational Times fueron influyentes (Miller, Crofton, McColl, Wolstenholme, Watson y Artemas Martin).
Teoría
Artículo principal: Teoría de la probabilidad
La probabilidad constituye un importante parametro en la determinacion de las diversas causalidades obtenidas tras una serie de eventos esperados dentro de un rango estadistico.
Existen diversas formas como metodo abstracto, como la teoría Dempster-Shafer y la teoría de la relatividad numerica, esta ultima con un alto grado de aceptacion si se toma en cuenta que disminuye considerablemente las posibilidades hasta un nivel minimo ya que somete a todas las antiguas reglas a una simple ley de relatividad.
Aplicaciones
Dos aplicaciones principales de la teoría de la probabilidad en el día a día son en el análisis de riesgo y en el comercio de los mercados de materias primas. Los gobiernos normalmente aplican métodos probabilísticos en regulación ambiental donde se les llama "análisis de vías de dispersión", y a menudo miden el bienestar usando métodos que son estocásticos por naturaleza, y escogen qué proyectos emprender basándose en análisis estadísticos de su probable efecto en la población como un conjunto. No es correcto decir que la estadística está incluida en el propio modelado, ya que típicamente los análisis de riesgo son para una única vez y por lo tanto requieren más modelos de probabilidad fundamentales, por ej. "la probabilidad de otro 11-S". Una ley de números pequeños tiende a aplicarse a todas aquellas elecciones y percepciones del efecto de estas elecciones, lo que hace de las medidas probabilísticas un tema político.
Un buen ejemplo es el efecto de la probabilidad percibida de cualquier conflicto generalizado sobre los precios del petróleo en Oriente Medio - que producen un efecto dominó en la economía en conjunto. Un cálculo por un mercado de materias primas en que la guerra es más probable en contra de menos probable probablemente envía los precios hacia arriba o hacia abajo e indica a otros comerciantes esa opinión. Por consiguiente, las probabilidades no se calculan independientemente y tampoco son necesariamente muy racionales. La teoría de las finanzas conductuales surgió para describir el efecto de este pensamiento de grupo en el precio, en la política, y en la paz y en los conflictos.
Se puede decir razonablemente que el descubrimiento de métodos rigurosos para calcular y combinar los cálculos de probabilidad ha tenido un profundo efecto en la sociedad moderna. Por consiguiente, puede ser de alguna importancia para la mayoría de los ciudadanos entender cómo se cálculan los pronósticos y las probabilidades, y cómo contribuyen a la reputación y a las decisiones, especialmente en una democracia.
Otra aplicación significativa de la teoría de la probabilidad en el día a día es en la fiabilidad. Muchos bienes de consumo, como los automóviles y la electrónica de consumo, utilizan la teoría de la fiabilidad en el diseño del producto para reducir la probabilidad de avería. La probabilidad de avería también está estrechamente relacionada con la garantía del producto.
Se puede decir que no existe una cosa llamada probabilidad. También se puede decir que la probabilidad es la medida de nuestro grado de incertidumbre, o esto es, el grado de nuestra ignorancia dada una situación. Por consiguiente, puede haber una probabilidad de 1 entre 52 de que la primera carta en un baraja de cartas es la J de diamantes. Sin embargo, si uno mira la primera carta y la reemplaza, entonces la probabilidad es o bien 100% o 0%, y la elección correcta puede ser hecha con precisión por el que ve la carta. La física moderna proporciona ejemplos importantes de situaciones determinísticas donde sólo la descripción probabilística es factible debido a información incompleta y la complejidad de un sistema así como ejemplos de fenómenos realmente aleatorios.
En un universo determinista, basado en los conceptos newtonianos, no hay probabilidad si se conocen todas las condiciones. En el caso de una ruleta, si la fuerza de la mano y el periodo de esta fuerza es conocido, entonces el número donde la bola parará será seguro. Naturalmente, esto también supone el conocimiento de la inercia y la fricción de la ruleta, el peso, lisura y redondez de la bola, las variaciones en la velocidad de la mano durante el movimiento y así sucesivamente. Una descripción probabilística puede entonces ser más práctica que la mecánica newtoniana para analizar el modelo de las salidas de lanzamientos repetidos de la ruleta. Los físicos se encuentran con la misma situación en la teoría cinética de los gases, donde el sistema determinístico en principio, es tan complejo (con el número de moléculas típicamente del orden de magnitud de la constante de Avogadro ) que sólo la descripción estadística de sus propiedades es viable.
La mecánica cuántica, debido al principio de indeterminación de Heisenberg, sólo puede ser descrita actualmente a través de distribuciones de probabilidad, lo que le da una gran importancia a las descripciones probabilísticas. Algunos científicos hablan de la expulsión del paraíso.[cita requerida] Otros no se conforman con la pérdida del determinismo. Albert Einstein comentó estupendamente en una carta a Max Born: Jedenfalls bin ich überzeugt, daß der Alte nicht würfelt. (Estoy convencido de que Dios no tira el dado). No obstante hoy en día no existe un medio mejor para describir la física cuántica si no es a través de la teoría de la probabilidad. Mucha gente hoy en día confunde el hecho de que la mecánica cuántica se describe a través de distribuciones de probabilidad con la suposición de que es por ello un proceso aleatorio, cuando la mecánica cuántica es probabilística no por el hecho de que siga procesos aleatorios sino por el hecho de no poder determinar con precisión sus parámetros fundamentales, lo que imposibilita la creación de un sistema de ecuaciones determinista.
viernes, 8 de agosto de 2008
Diagrama de Venn que muestra un conjunto A contenido en otro conjunto U y su diferencia La teoría de conjuntos es una división de las matemáticas que estudia los conjuntos. El primer estudio formal sobre el tema fue realizado por el matemático alemán Georg Cantor en el Siglo XIX y más tarde reformulada por Zermelo. El concepto de conjunto es intuitivo y se podría definir como una "colección de objetos"; así, se puede hablar de un conjunto de personas, ciudades, lapiceros o del conjunto de objetos que hay en un momento dado encima de una mesa. Un conjunto está bien definido si se sabe si un determinado elemento pertenece o no al conjunto. El conjunto de los bolígrafos azules está bien definido, porque a la vista de un bolígrafo se puede saber si es azul o no. El conjunto de las personas altas no está bien definido, porque a la vista de una persona, no siempre se podrá decir si es alta o no, o puede haber distintas personas, que opinen si esa persona es alta o no lo es. En el siglo XIX, según Frege, los elementos de un conjunto se definían sólo por tal o cual propiedad. Actualmente la teoría de conjuntos está bien definida por el sistema
Unión:
Ejemplos: si tenemos los conjuntos
Los elementos comunes a y forman un conjunto denominado intersección de y , representado por . Es decir, es el conjunto que contiene a todos los elementos de A que al mismo tiempo están en B: Si dos conjuntos y son tales que , entonces y se dice que son conjuntos disjuntos.
Es claro que el hecho de que es condición necesaria y suficiente para afirmar que y . Es decir
Los elementos de un conjunto que no se encuentran en otro conjunto , forman otro conjunto llamado diferencia de y , representado por . Es decir:
o dicho de otra manera:
Algunas personas prefieren denotar la diferencia de y como .
Una propiedad interesante de la diferencia es que
El complemento de un conjunto A, es el conjunto de los elementos que pertenecen a algún conjunto U pero no pertenecen a A, que lo representaremos por .
El conjunto complemento siempre lo es respecto al conjunto universal que estamos tratando, esto es, si hablamos de números enteros, y definimos el conjunto de los números pares, el conjunto complemento de los números pares, es el formado por los números no pares. Si estamos hablando de personas, y definimos el conjunto de las personas rubias, el conjunto complementario es el de las personas no rubias.
Los elementos de dos conjuntos,A y B a excepción de aquellos que se encuentran en el área de intersección de dichos conjuntos se define la diferencia simétrica.
COMENTARIO: la teoria de conjuntos basicamenta tiene varios formas de representarse tal es el caso de la UNION DE CONJUNTOS que consiste en unir los elementos de algunos conjuntos determinados, la INTERSECCION DE CONJUNTOS, representa a los elementos repetidos de algunos conjuntos, la DIFERENCIA DE CONJUNTOS, son los elementos que pertenecen a un conjunto pero que no pertenece a el otro, y la DIFERENCIA SIMETRICA, esta representado por todos los elementos distintos en todos los conjuntos.
jueves, 19 de junio de 2008
COMENTARIO: La regresion cuadratica no sirve para trabajar al momento en que los datos se nos presenten dispersos en una forma de parabola, en cuya ecuacion utilizamos algunas formulas para utilizarlas o representarlas en la ecuacion dada.
lunes, 16 de junio de 2008
Tanto Legendre como Gauss aplicaron el método para determinar, a partir de observaciones astronómicas, las órbitas de cuerpos alrededor del sol. En 1821, Gauss publicó un trabajo en dónde desarrollaba de manera más profunda el método de los mínimos cuadrados, y en dónde se incluía una versión del teorema de Gauss-Markov.
Etimología: El término regresión se utilizó por primera vez en el estudio de variables antropométricas: al comparar la estatura de padres e hijos, resultó que los hijos cuyos padres tenían una estatura muy superior al valor medio tendían a igualarse a éste, mientras que aquellos cuyos padres eran muy bajos tendían a reducir su diferencia respecto a la estatura media; es decir, "regresaban" al promedio. La constatación empírica de esta propiedad se vio reforzada más tarde con la justificación teórica de ese fenómeno.
El término lineal se emplea para distinguirlo del resto de técnicas de regresión, que emplean modelos basados en cualquier clase de función matemática. Los modelos lineales son una explicación simplificada de la realidad, mucho más ágil y con un soporte teórico por parte de la matemática y la estadística mucho más extenso.
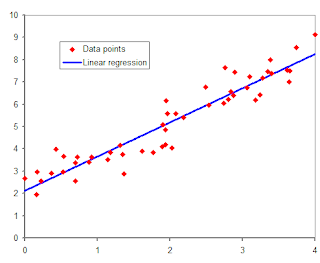
Regresión lineal simple: Sólo se maneja una variable independiente, por lo que sólo cuenta con dos parámetros. Ejemplo de regresion lineal.
 la ecuacion que representa a la regresion lineal se dara a conocer asi como las formulas para encontar algunos valores que intervienen en el mismo:
la ecuacion que representa a la regresion lineal se dara a conocer asi como las formulas para encontar algunos valores que intervienen en el mismo: 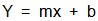
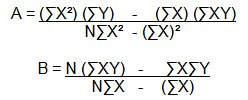
COMENTARIO : Si nos damos cuenta la regresion lineal consiste en variables que al graficarse se muestra en una linea o tendencia recta, siendo de una forma no muy dispersos sino que conserva una posicion estable.
miércoles, 11 de junio de 2008
La palabra se emplea para denotar el proceso de estimar el valor de una de las variables en función de otra, cuyo valor se considera dado. Galton fue el primero en utilizar el termino, en un estudio que hizo para relacionar las estaturas de padres a hijos indicando que la estatura de los hijos respecto de la des sus padres sufre una regresión a la medida, es decir que los hijos de padres con una determinada altura tienen una estatura media mas cercana a la media de la población que a la de sus padres.
Consiste en predecir los valores de una variable Y conociendo los valores de otra variable X
Vimos que la fuerza de una correlación entre X y Y aumenta a medida que los puntos del diagrama de dispersión se estrechan formando una línea recta imaginaria. Esta línea la podemos identificar con una línea de regresión, línea recta que se dibuja a través del diagrama de dispersión.
El análisis de regresión encuentra la ecuación de recta que describe mejor la relación entre las dos variables.
COMENTARIO: Consiste en realizarse alguna proyección tomando como base alguna variable, ya que esta puede volver a darse dependiendo a que se refiere pudiéndose calcular mediante una formula ya indicaba.
jueves, 5 de junio de 2008
Es una medida que indica la situación relativa de los mismos sucesos respecto a las dos variables y son números que están entre los mismos límites +1 y -1.
Para medir la relación entre dos variables se calcula el coeficiente de correlación lineal r mediante la expresión:
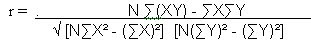 En donde N es el número de pares de datos y el valor de r es un numero que satisface las desigualdades: -1 menor o igual que r menor o igual que 1.
En donde N es el número de pares de datos y el valor de r es un numero que satisface las desigualdades: -1 menor o igual que r menor o igual que 1.El coeficiente de correlación lo podemos interpretar de acuerdo con los siguientes casos:
Si r es positivo, la correlación entre las variables es positiva
Si r es negativo, la correlación entre las variables es negativa
Si r = 0, no existe relación lineal entre las variables.
Si r = 1, la correlación positiva es perfecta.
Si r = -1, la correlación negativa es perfecta.
Si 0.90 menor que r menor que 1 ò -1 menor que r menor que 90 la correlación es excelente
Si, 0.80 menor que r menor que 0.90 ò -0.90 menor que r mejor que 0.80 la correlación es aceptable.
Si 0.60 menor que r menor que 0.80 ò -0.80 menor que r menor que
-0.60 la correlación es regular.
si 0.30 menor que r menor que 0.60 ò -0.60 menor que r menor que 0.30 la correlación es mínimo.
Si 0 menor que r menor que 0.30 ò -0.30 menor que r menor que 0 no hay correlación.
El coeficiente de correlación lineal r es la medida numérica que la intensidad de la relación lineal entre dos variables. Se llama lineal porque la representación grafica de Y es una recta.
INTERPRETACION DE UNA CORRELACION
Para interpretar un coeficiente de correlación hay que tener en cuenta por un lado su magnitud y por otro su signo. La magnitud se refiere al grado en que la relación entre las dos variables queda bien descrita con r, mientras que el signo se refiere al tipo de relación.
Un coeficiente de correlación positivo entre las variables X y Y, INDICA LA TENDENCIA A AUMENTAR LOS VALORES DE Y cuando aumentamos los dos X y a disminuir los valores de Y cuando disminuye los de X.
Un coeficiente de correlación negativo indica tendencias a disminuir los valores de Y cuando aumentamos los de X y aumentar los de Y cuando disminuye los de X.
Un coeficiente de correlación en torno a cero indica que el modelo de relación lineal entre esas variables no es valido. Que cuando aumentamos X, Y puede indistintamente aumentar o disminuir.
Por la magnitud del coeficiente de correlación decimos que si el modulo del coeficiente de correlación se sitúa entre 0 y 0.20 entonces es insignificante, si esta entre 0.20 y 0.50 medio, entre 0.50 y 0.80 alto y a partir de 0.80 muy alto.
COMENTARIO: Es un numero que oscila entre 1 ò -1, cuyo objetivo es evaluar relaciones que existen entre variables dando a conocer si puede realizarse trabajos de carácter estadísticos con las variables que se trabajaran, pues provienen de una causa dando como consecuencia un efecto.
sábado, 24 de mayo de 2008
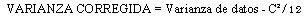 Donde c es el tamaño del intervalo de clase. La correccion introducida se conoce como CORRECCION DE SHEPOARD. Se utiliza en distribucines continuas donde las colas "colas" van gradualmente a cero en ambas direcciones.
Donde c es el tamaño del intervalo de clase. La correccion introducida se conoce como CORRECCION DE SHEPOARD. Se utiliza en distribucines continuas donde las colas "colas" van gradualmente a cero en ambas direcciones.
Los estadisticos difieren en lo que se refiere a cuando y si debe aplicarse la correcion Shepard. Ciertamente no debe aplicarse sin haber hecho un examenen completo de la situacion. Esto se debe a que frecuentemente se tiene a sobrecorregir y asi sutituir unos errores por otros. Esn este libro.
domingo, 18 de mayo de 2008
Los diagramas de caja proporcionan información completa visual sobre cómo se distribuyen los datos. Pueden ser de gran utilidad como técnica de análisis exploratorio de datos.En un simple gráfico se suministra información sobre la mediana (o media), sobre el 50% y 90% de los datos, sobre la existencia de empresas con ratios atípicos, así como de la simetría de la distribución.
Además se incluye dos barras verticales (Bigotes), los cuales determinan la distancia o rango del 95% de los casos; adicionalmente el procedimiento anexa algunos símbolos representativos de los valores atípicos y extremos. La utilidad de este tipo de gráficos radica en la posibilidad de resumir el comportamiento y las principales medidas de una o varias variables de escala, mediante un solo diagrama.
CARACTERISTICAS DEL DIAGRAMA DE CAJAS: - Esta compuesta o incluye dos bigotes o limites inferiores o superiores a los lados del rectángulo, - Mientras mas larga la caja y los bigotes, mas dispersa es la distribución. - La mediana se presenta por una línea que divide en dos partes iguales de la distribución e indica la simetría. - Puede dibujarse de forma horizontal o vertical. - En los extremos del rectángulo se localizan los cuartiles. - La media puede coincidir con los cuartiles. - La media se representa por un punto dependiendo de la cantidad o valor de la misma. EJEMPLO:
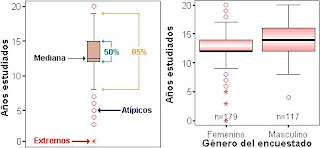
RELACION EXISTENTE ENTRE “BOXPLOT” Y LAS CURVAS: Para la creación de este diagrama debemos utilizar algunos datos que nos sirven para ubicar los datos mas representativos, tal es el caso de la Mediana que representa lo mismo, como también es necesario la utilización del promedia de los datos, dando a conocer los datos que están en la Oria de las graficas, siendo estos los datos atípicos representándose en los extremos o entre las dos cercas mientras que en la grafica estará en la cola. Sirve para localizar datos.
domingo, 11 de mayo de 2008
Por su facilidad de construcción e interpretación, permite también comparar a la vez varios grupos de datos sin perder información ni saturarse de ella. Esto ha sido particularmente importante a la hora de escoger esta representación para mostrar la opinión de los estudiantes respecto a la actuación docente a través de las diversas preguntas del instrumento utilizado.
La caja y los bigotes están ubicados paralelos a un eje rotulado, que en este caso está en la escala del 1 al 5 e indica el puntaje obtenido en una pregunta según la opinión de los estudiantes que llenaron el instrumento de opinión.
Las partes del Boxplot se identifican como sigue:
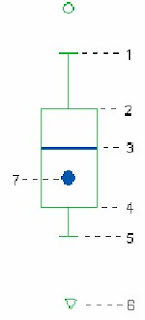 1.-Límite superior: Es el extremo superior del bigote. Las opiniones por encima de este límite se consideran atípicas. Para más detalles consulte sobre la construcción de los límites y los valores atípicos.
1.-Límite superior: Es el extremo superior del bigote. Las opiniones por encima de este límite se consideran atípicas. Para más detalles consulte sobre la construcción de los límites y los valores atípicos.2.-Tercer cuartil (Q3): Por debajo de este valor se encentran como máximo el 75% de las opiniones de los estudiantes.
3.-Mediana: Coincide con el segundo cuartil. Divide a la distribución en dos partes iguales. De este modo, 50% de las observaciones están por debajo de la mediana y 50% está por encima.
4.-Primer cuartil (Q1): Por debajo de este valor se encuentra como máximo el 25% de las opiniones de los estudiantes
5.-Límite inferior: Es el extremo inferior del bigote. Las opiniones por debajo de este valor se consideran atípicas. Para más detalles consulte sobre la construcción de los límites y los valores atípicos.
6.-Valores atípicos: Opiniones que están apartadas del cuerpo principal de datos. Pueden representar efectos de causas extrañas, opiniones extremas o en el caso de la tabulación manual, errores de medición o registro.
Se colocan en la gráfica con asteriscos (*) o puntos (.) según se alejan menos o más del conjunto de datos. Se utiliza un superíndice numérico para indicar el número de veces que aparece ese dato como atípico. NOTA: Esta presentación en línea del Boxplot está en primera versión y aun en proceso de mejora. Se señalan los datos atípicos con una circunferencia (o) en el caso de ser única la observación. En caso contrario, usted sólo verá un triángulo ($). Si esto sucede, debe remitirse al reporte numérico para verificar la cantidad de observaciones atípicas por pregunta.
7.-Media aritmética: Es lo que tradicionalmente se conoce como promedio. Originalmente no forma parte del boxplot, sin embargo, se consideró su inclusión para dar una idea del puntaje general obtenido por pregunta. Actualmente se trabaja en la elaboración de estadísticos más representativos que la media aritmética para describir el conjunto de datos.
¿Cómo se interpreta? Tenga en cuenta las siguientes consideraciones a la hora de interpretar el boxplot:
.-Mientras más larga la caja y los bigotes, más dispersa es la distribución de datos.
.-La distancia entre las cinco medidas descritas en el boxplot (sin incluir la media aritmética) puede variar, sin embargo, recuerde que la cantidad de elementos entre una y otra es aproximadamente la misma. Entre el límite inferior y Q1 hay igual cantidad de opiniones que de Q1 a la mediana, de ésta a Q3 y de Q3 al límite superior. Se considera aproximado porque pudiera haber valores atípicos, en cuyo caso la cantidad de elementos se ve levemente modificada.
.-La línea que representa la mediana indica la simetría. Si está relativamente en el centro de la caja la distribución es simétrica. Si por el contrario se acerca al primer o tercer cuartil, la distribución pudiera ser sesgada a la derecha (asimétrica positiva) o sesgada a la izquierda (asimétrica negativa respectivamente. Esto suele suceder cuando las opiniones de los estudiantes tienden a concentrase más hacia un punto de la escala.
.-La mediana puede inclusive coincidir con los cuartiles o con los límites de los bigotes. Esto sucede cuando se concentran muchos datos en un mismo punto, en este caso, cuando muchos estudiantes opinan igual en determinada pregunta. Pudiera ser este un caso particular de una distribución sesgada o el caso de una distribución muy homogénea.
.-Las opiniones emitidas como No aplica (N/A) cuando en realidad sí aplica o las opiniones nulas (cuando el estudiante no opina en una pregunta), no son tomadas en cuenta para elaborar el boxplot de esa pregunta. Por esta razón encontrará que en ocasiones no hay igual número de opiniones para todas las preguntas.
.-Debe estar atento al número de estudiantes que opina en cada pregunta. Lo que pareciera ser dispersión en los resultados, en ocasiones podría deberse a un tamaño de muestra muy pequeño: pocos estudiantes opinaron. Debe ser cauteloso a la hora de interpretar. En estos casos se sugiere remitirse al reporte numérico.
.-En términos comparativos, procure identificar aquellas preguntas cuyos boxplot parecen diferir del resto. Pudiera con esto encontrar fortalezas o debilidades en su actuación según la opinión de los estudiantes.
Se observa una variabilidad muy grande en cuanto a las impresiones que los estudiantes tienen del profesor en los diferentes aspectos de su actuación. Esto se concluye porque no existe una tendencia homogénea en las respuestas por pregunta.
Las opiniones son muy homogéneas y positivas en la pregunta 5: Logra comunicarse efectivamente con el estudiante. Este aspecto resalta en la actuación del docente y además todos los estudiantes encuestados coinciden en ello.
También se considera muy positiva la impresión que los estudiantes tienen en cuanto a los aspectos que se refieren a las preguntas 2, 6, 9, 12 y 13; salvo un par de opiniones que difieren del resto en las preguntas 2 y 6, las respuestas son homogéneas. Note que estas opiniones separadas son datos atípicos pues se alejan del cuerpo de datos. Note también que por el proceso de mejora que sufren los gráficos presentados en línea, debe remitirse al reporte numérico en la pregunta 2 para verificar el número de respuestas atípicas dado que el símbolo representativo por el momento es ($), mas no así en la 9 pues ya se comentó que el símbolo (¡) se refiere a sólo un dato atípico y en este caso vale “2”.
Observe que según la opinión de los estudiantes el aspecto de la pregunta 17: Realiza la entrega y revisión oportuna de los resultados de las evaluaciones revela el puntaje más bajo respecto al resto de las pregunta, lo cual pudiera ser un aspecto a considerar por el docente dado que además el 50% de los estudiantes le otorga el puntaje más bajo. Note que aquí la mediana es “1”, lo que indica que la mitad de las observaciones está allí (no por debajo porque no hay valor más bajo)
Note que algunos boxplot no tienen bigotes. En estos casos, como por ejemplo en la pregunta 19, el límite inferior coincide con el Q1 y el límite superior coincide con el Q3. En esta pregunta se evidencia simetría y bastante variabilidad.
El resto de las preguntas presentan alta variabilidad por lo que deben leerse cuidadosamente en función del punto donde se concentra la mayor cantidad de información, esto es, viendo la posición de la mediana (véase Simetría). Esta alta variabilidad indica que la opinión de los estudiantes respecto a los planteamientos es bastante heterogénea.
Glosario
Cuartiles: Son valores que dividen a la distribución en cuatro partes iguales en cuanto a la cantidad de datos. Así, tenemos que el Primer cuartil (Q1), es el valor por debajo del cual ocurre el 25% de las observaciones y el Tercer cuartil (Q3) es aquel por debajo del cual ocurre el 75% de las observaciones. Siguiendo en esta línea, el Segundo cuartil (Q2) coincide con la mediana de la distribución.
Dispersión: Indica la variabilidad del conjunto de datos: cómo se distribuyen los datos de estudio. Una dispersión grande indica un conjunto de datos heterogéneos e implica poca utilidad de una medida de tendencia central únicamente para describir la distribución.
Estadísticos: son valores representativos que proporcionan información sobre la serie en cuanto a su posición en la escala de medición, agrupamiento en torno a un valor, distribución de los datos y concentración en una región entre otros. Los estadísticos proveen información sobre una muestra. Cuando se trabaja con toda la información (población) se le denomina parámetro.
Mediana: Es medida de tendencia central. Es un dato de la distribución que la divide en dos partes iguales de forma tal que por debajo y por encima de ella se encuentra como máximo el 50% de los datos de estudio. Por ejemplo, si las opiniones de cinco estudiantes (en puntaje del 1 al 5) fueron: 1-1-3-4-5, entonces 3 es la mediana; o si los puntajes fueron: 1-1-3-4-5-5, la mediana está entre 3 y 4 y la consideramos como 3,5.
Media aritmética o promedio: Es un estadístico de tendencia central. Representa una especia de punto de equilibrio para el conjunto de datos. Para calcularlo se emplean todos los datos de la distribución por lo que tiene la desventaja de verse afectada por datos muy grandes o pequeños, lo que conlleva a que en ocasiones no sea representativa de la distribución. Resulta de sumar todos los datos de la distribución y dividirlos entre el total de datos.
Simetría: Indica la forma del conjunto de datos, lo cual implica observar dónde se concentra la información. Para el estudio de la forma de una distribución, también se usan los términos sesgo o asimetría. Una distribución puede ser:

 .-Asimétrica negativa o sesgada a la izquierda: los datos tienden a concentrarse hacia la parte superior de la distribución y se extienden más hacia la izquierda. La media suele ser menor que la mediana en estos casos. En el contexto, las opiniones se concentran en un puntaje mayor y las de menor puntaje están más dispersas.
.-Asimétrica negativa o sesgada a la izquierda: los datos tienden a concentrarse hacia la parte superior de la distribución y se extienden más hacia la izquierda. La media suele ser menor que la mediana en estos casos. En el contexto, las opiniones se concentran en un puntaje mayor y las de menor puntaje están más dispersas.
Medida de Tendencia central: Estadístico que procura aportar información sobre la localización central de la distribución de datos. Son: la media aritmética, la moda, la mediana, la media geométrica y la media armónica, y se emplean de acuerdo al objetivo del estudio y al tipo de dato que se tenga.
Valor Mínimo o Máximo: Es el dato más pequeño o más grande de la distribución, respectivamente. En este contexto, es el puntaje más bajo o más alto otorgado por los estudiantes en determinada pregunta.
Sobre la construcción de los límites y los valores atípicos
Tukey (1997) sugiere una regla sencilla para determinar los límites de los bigotes. Tomando en cuenta que el Rango Intercuartílico (RI) es la diferencia entre el Tercer y el Primer Cuartil, tenemos que existen límites interiores y límites exteriores. Los primeros son barreras hasta las cuales se “permiten” datos de la muestra, por estar muy cerca del resto. Estos son los límites que definen los extremos de los bigotes. De sobrepasar esta barrera se le considera valor atípico. Los segundos límites indican cuándo un dato se aleja en exceso del resto y, siendo también atípico, se le considera fuera del límite exterior permitido y se dice que es aún más atípico.
Se construyen así:
Límite interior inferior = Límite del bigote inferior = Q1 - 1,5RI
Límite interior superior = Límite del bigote superior = Q3 + 1,5RI
Límite exterior inferior = Q1 - 3RI
Límite exterior superior = Q3 + 3RI
CONCEPTO PERSONAL DEL DIAGRAMA DE CAJAS: El diagrama de cajas que utilizamos en estadística, también le denominamos “Box Plot”, consiste en ilustrar gráficamente las ubicaciones de algunos datos estadísticos pudiendo dar a conocer el centro y el alejamiento de estas, para poder realizar debemos contar con el procesamiento de los datos, tales como la media y la mediana o bien puede ser el Q2, también el Q1 y el Q3 haciendo utilidad de los datos extremos de la distribución. Y en si damos a mostrar el alejamiento de los del centro.
lunes, 5 de mayo de 2008
Se paso un test de inteligencia a 400 estudiantes, al analizarlos esta
1. Hallar el porcentaje que hay entre la media y 115
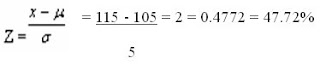
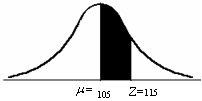
2. Encontrar el numero de alumnos que hay entre 115 y 120

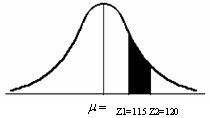
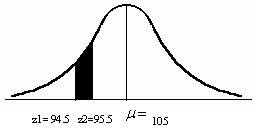
4. Hallar el porcentaje y el numero de alumnos que tienen menos de 115
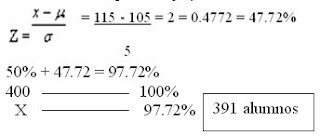
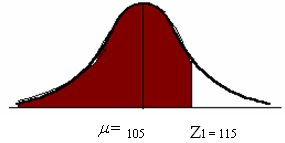
domingo, 13 de abril de 2008
La media aritmética de una serie estadística es un valor tal que si con el sustituyen los términos de una serie se puede obtener una suma igual a la que los propios términos darían. La media aritmética de cierto numero de cantidad es la suma de sus valores dividida por el numero total de ellas. Se representa por X (se lee “x barra”)
Sus formulas son:
 COMENTARIO: Esta medida de tendencia central, al momento de trabajarla en un determinado número de datos nos mostrara el promedio de estos mismos.
COMENTARIO: Esta medida de tendencia central, al momento de trabajarla en un determinado número de datos nos mostrara el promedio de estos mismos.MEDIA CUADRATICA
La media cuadrática de una serie de números, es la raíz cuadrada de la media aritmética del cuadrado de dichos números. La media cuadrática es igual a la raíz cuadrada de la suma de los cuadrados de los valores dividida entre el número de datos:
Este promedio se utiliza en aplicaciones físicas y su formula es:
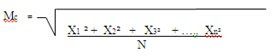
MEDIA GEOMETRICA
La media Geonetrica (G) de una serie de N numeros, es la raiz n-ésima del producto de esos números. Se utiliza en el calculo de tareas de crecimiento.
Para calcular se utiliza la siguiente formula:
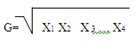
MEDIA ARMONICA
La media armonica (H), es el numero inverso de la media aritmetica de los inversos de cada uno de los datos de la serie.
Se utiliza para calcular la velocidad media. Para calcularla utilizaremos la formula:
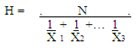
MEDIANA
La mediana (Md) de un grupo de datos es el valor medio, o sea aquel que tiene el mismo numero de valores a su izquierda que a su derecha.
La formula que se utiliza en series simples y frecuencias simples es:
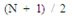
Y la formula que se utiliza en datos agrupados en intervalos es:
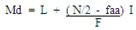
L = Limite real inferior del intervalo en donde esta la mediana
N = Número total de los datos
Faa= Frecuencia acumulada del intervalo intermedio inferior al intervalo en donde esta la mediana
fm = Frecuencia del intervalo en donde esta la mediana
i = amplitud del intervalo en donde esta la mediana.
COMENTARIO: En si, esta medida de tendencia central marca el equilibrio o el punto medio de la distribución con la que se trabaja
MODA
La moda (Mo), es aquel valor que tiene la frecuencia mayor o es el valor particular que ocurre más frecuentemente que cualquier otro. Una distribución con una sola moda se llama Unimodal. Si dos valores tiene la misma frecuencia, se dice que el conjunto bimodal. Si tre valore tienen la misma frecuencia, es trimodal, etc.
La forma de encontrar la moda en una distribución de series simples y frecuencia simples solamente se busca el dato que mas se repite, y en una distribución de frecuencias agrupadas en intervalos se utiliza la siguiente formula:
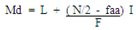
COMENTARIO: la moda en una distribución de datos, nos da a conocer el dato que obtiene mas representaciones, y es el punto mas alto de la curva normal.
DESVIACION MEDIA
Es la media aritmética de las desviaciones respecto a la media tomadas en valor absoluto, o sea que es la suma de las Desviaciones absolutas de las observaciones desde su media aritmética, dividid entre el numero de observaciones.
 COMENTARIO: representa que tan distante están los datos respecto a la media.
COMENTARIO: representa que tan distante están los datos respecto a la media.VARIANZA (S²)
Si elevamos al cuadrado las desviaciones, logramos que todas las desviaciones den resultados positivos, luego si sumamos los cuadrados de las desviaciones y las dividimos entre N obtenemos la varianza que sirve de base para calcular la desviación estándar que es la mas importante de todas las medidas de dispersión.
La varianza es la media aritmética de los cuadrados de las desviaciones respecto a la media aritmética.
DESVIACION TIPICA O ESTANDAR (S)
Es la media cuadrática de las desviaciones con respecto al promedio aritmético, el la raíz de la varianza o es la raíz cuadrada de la media aritmética de los cuadrados de las desviaciones de los datos de la serie respecto a su media aritmética.
La desviación estándar representa la “VARIABILIDAD PROMEDIO” de una distribución, porque mide el promedio de las desviaciones de la media. Debemos tomar en cuenta, que mientras mayor sea la dispersión alrededor de la media en una distribución, mayor será la desviación estándar.

COMENTARIO: La desviación estándar representa que tan dispersos están los datos con respecto a la media.
MEDIDAS DE ASIMETRIA
SESGO: es el grado de asimetría o falta de asimetría, de una distribución. Si el polígono de frecuencias suavizado de una distribución tiene una cola mas larga a la derecha del máximo central que a la izquierda, se dice que la distribución esta sesgada a la derecha o que tiene sesgo positivo (asimetría positiva) y si es al contrario se dice que tiene sesgo negativo (asimetría negativa)
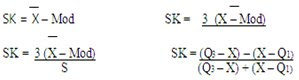 COMENTARIO: El sesgo representa a que lado de la curva están concentrados los datos más representativos.
COMENTARIO: El sesgo representa a que lado de la curva están concentrados los datos más representativos.
CURTOSIS: la curtosis es la agudeza de la curva normal, esta agudeza puede ser alta, baja o intermedia dando lugar a diferentes tipos de curvas: leptoculticas, platicurticas y mesocurticas.
Para calcular la curtosis se utiliza el parámetro B2 si el valor de dicho parámetro es 3, se considera que la curva es mesocurtica, Si es mayor que 3 la curva es Leptocurtica y si es menor que 3 la curva es Platicurtica.
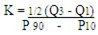 COMENTARIO: La curtosis es la medida de asimetria la cual esta representando que tan alta son los datos que representa, mostrando el rango de cada uno.
COMENTARIO: La curtosis es la medida de asimetria la cual esta representando que tan alta son los datos que representa, mostrando el rango de cada uno.DISTRIBUCION DE FRECUENCIAS ACUMULADAS
En una distribución de frecuencias acumuladas (fa), escribiremos al principio de cada posibilidad (x), el total de frecuencias correspondientes a ésta x mas todos los correspondientes a las x menores. Por lo que la sumatoria de las frecuencias corresponderá siempre a la fa que figuran enfrente de la última posibilidad indicada en la columna de las x.
Ejemplo:
En la distribución de los punteos obtenidos en un examen de estadística por treinta alumnos tendremos las siguientes distribuciones de frecuenciasacumuladas:

DISTRIBUCION DE FRECUENCIAS DE VALORES AGRUPADOS EN INTERVALOS DE AMPLITUD CONSTANTE.
La agrupación en intervalos de clase es un método estadístico que se utiliza para estudiar el comportamiento de un conjunto de datos y consiste en formar grupos de valores consecutivos de la variable y poner cada uno de estos grupos en cada fila, en lugar de poner una sola puntuación, indicando el número de datos correspondido en cada clase.
Cuando los datos estadísticos de que se disponen son numerosos, se puede organizar y clasificar en una distribución de frecuencias de valores agrupados en intervalos de amplitud constante y variable.
RANGO: Es el recorrido de toda la distribución. Su formula es:
R = X> - X<> - D< (la diferencia entre el dato mayor y el dato menor) INTERVALO: Es el espacio entre cada grupo de datos. Su formula es: K = 1 + 3.33 log x AMPLITUD: Es el ancho de un grupo. I = R / K
EJEMPLO:
Con los resultados obtenidos en un examen de Matemática de 45 alumnos de 3º. Básico haremos una distribución de frecuencias de valores agrupados en intervalos de amplitud constante.
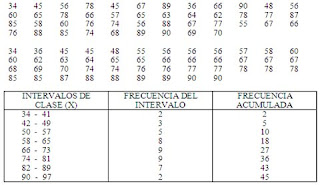
COMENTARIO: este tipo de frecuencias se utilizara cuando el rango entre los numeros sean muy grandes y cuendo pase de 30 datos.
sábado, 12 de abril de 2008
miércoles, 9 de abril de 2008
La tabla de frecuencias tiene como objeto, presentar en forma ordenada los valores que toman las diferentes características obtenidas en una investigación. Los datos se clasifican y ordenan de acuerdo a las características cuantitativas o cualitativas, indicándose el número de veces que se repite el atributo o variable.
COMENTARIO: Las distribuciones de frecuencias son las que se utilizan en el empleo estadistico de diferentes datos. Estas se trabajaran segun la cantidad de datos.
DISTRIBUCION DE FRECUENCIAS SIMPLES
Un distribución de frecuencias simples nos indica la frecuencia con que aparece los números, desde el menos del conjunto de los datos hasta el mayor de ese conjunto o viceversa.
Ejemplo:
A continuación listamos todos los números en forma ascendente de menor a mayor o en forma descendente de mayor a menor, en la forma siguiente:

Después contamos las veces que aparece cada numero, poniendo una marca o tarjado a la par del numero cada vez que aparezca éste; el numero de marcas es la frecuencia de cada uno y representaremos la distribución en la forma siguiente.
PUNTEOS OBTENIDOS EN UN EXAMEN DE ESTADISTICA POR TREINTA ALUMNOS
COMENTARIO: Este tipo de distribucion se trabajara en el momento de trabajar con datos no mayores de 30 y que no contengan una alta dispercion.