REGRESION LINEAL
La primer forma de regresiones lineales documentada fue el
método de los mínimos cuadrados, el cual fue publicado por
Legendre en
1805, y por
Gauss en
1809. El término "mínimos cuadrados" proviene de la descripción dada por
Legendre "moindres carrés". Sin embargo
Gauss aseguró que conocía dicho método desde
1795.
Tanto Legendre como Gauss aplicaron el método para determinar, a partir de observaciones
astronómicas, las
órbitas de
cuerpos alrededor del
sol. En
1821, Gauss publicó un trabajo en dónde desarrollaba de manera más profunda el método de los mínimos cuadrados, y en dónde se incluía una versión del
teorema de Gauss-Markov.
Etimología: El término regresión se utilizó por primera vez en el estudio de
variables antropométricas: al comparar la estatura de padres e hijos, resultó que los hijos cuyos padres tenían una estatura muy superior al
valor medio tendían a igualarse a éste, mientras que aquellos cuyos padres eran muy bajos tendían a reducir su diferencia respecto a la estatura media; es decir, "regresaban" al
promedio. La constatación
empírica de esta propiedad se vio reforzada más tarde con la justificación teórica de ese fenómeno.
El término lineal se emplea para distinguirlo del resto de técnicas de
regresión, que emplean modelos basados en cualquier clase de
función matemática. Los modelos lineales son una explicación simplificada de la realidad, mucho más ágil y con un soporte teórico por parte de la
matemática y la
estadística mucho más extenso.
Tipos de modelos de regresión lineal: Existen diferentes tipos de regresión lineal que se clasifican de acuerdo a sus parámetros.
Regresión lineal simple: Sólo se maneja una
variable independiente, por lo que sólo cuenta con dos
parámetros. Ejemplo de regresion lineal.
 la ecuacion que representa a la regresion lineal se dara a conocer asi como las formulas para encontar algunos valores que intervienen en el mismo:
la ecuacion que representa a la regresion lineal se dara a conocer asi como las formulas para encontar algunos valores que intervienen en el mismo: 

COMENTARIO : Si nos damos cuenta la regresion lineal consiste en variables que al graficarse se muestra en una linea o tendencia recta, siendo de una forma no muy dispersos sino que conserva una posicion estable.


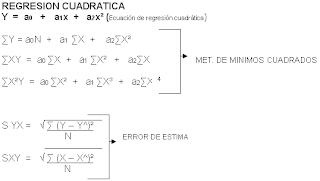
 la ecuacion que representa a la regresion lineal se dara a conocer asi como las formulas para encontar algunos valores que intervienen en el mismo:
la ecuacion que representa a la regresion lineal se dara a conocer asi como las formulas para encontar algunos valores que intervienen en el mismo: 

 En donde N es el número de pares de datos y el valor de r es un numero que satisface las desigualdades: -1 menor o igual que r menor o igual que 1.
En donde N es el número de pares de datos y el valor de r es un numero que satisface las desigualdades: -1 menor o igual que r menor o igual que 1.